다이나믹 프로그래밍

다이나믹 프로그래밍 (DP)

큰 문제를 부분 문제로 나눈 후 답을 찾아가는 과정에서, 계산된 결과를 기록하고 재활용하며 문제의 답을 구하는 방식
중간 계산 결과를 기록하기 위한 메모리가 필요
한 번 계산한 부분을 다시 계산하지 않아 속도가 빠름

다른 알고리즘과의 차이점

분할 정복과의 차이
분할 정복은 부분 문제가 중복되지 않음
DP는 부분 문제가 중복되어 재활용에 사용
그리디 알고리즘과의 차이
그리디 알고리즘은 순간의 최선을 구하는 방식 (근사치)
DP는 모든 방법을 확인 후 최적해 구하는 방식

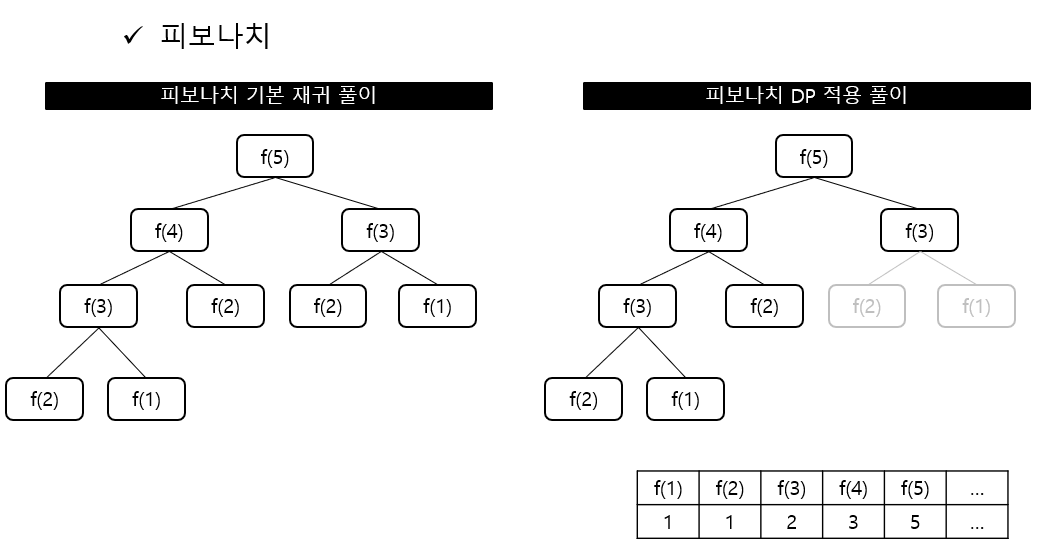
다이나믹 프로그래밍 예시

다이나믹 프로그래밍 방법

타뷸레이션 (Tabulation)
상향식 접근 방법
작은 하위 문제부터 풀면서 올라감
모두 계산하면서 차례대로 진행
메모이제이션 (Memoization)
하향식 접근 방법
큰 문제에서 하위 문제를 확인해가며 진행
계산이 필요한 순간 계산하며 진행

피보나치 수열 (일반 풀이 - O(n^2))

피보나치 수열 (DP 풀이 - 타뷸레이션 - O(n))

피보나치 수열 (DP 풀이 - 메모이제이션)

// 알고리즘 - 다이나믹 프로그래밍

public class Main {
    // 피보나치 수열 (일반 풀이 - O(n^2))
    // 계산했던 부분도 다시 계산
    public static int fib(int n) {
        if (n <= 1) {
            return n;
        } else {
            return fib(n - 1) + fib(n - 2);
        }
    }

    // 피보나치 수열 (DP 풀이 - 타뷸레이션 - O(n))
    public static int fibDP(int n) {
        // DP 용 메모리 필요
        int[] dp = new int[n < 2 ? 2 : n + 1];
        dp[0] = 0;
        dp[1] = 1;

        // 저장한 값 기반으로 피보나치 수열 계산
        // 테이블을 채워나가는 방식
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }


    // 피보나치 수열 (DP 풀이 - 메모이제이션)
    static int[] dp = new int[8];
    public static int fibDP2(int n) {
        if (n <= 2) {
            return 1;
        }

        // 기록해둔 게 있으면 사용
        if (dp[n] != 0) {
            return dp[n];
        }

        // 없으면 하위 호출
        dp[n] = fibDP2(n - 1) + fibDP2(n - 2);
        return dp[n];
    }

    public static void main(String[] args) {
        // Test code
        System.out.println(fib(7));
        System.out.println(fibDP(7));
        System.out.println(fibDP2(7));
    }
}

13
13
13

문제풀이

// Practice
// 정수 n 이 주어졌을 때 아래의 연산을 통해 1로 만들려고 한다.
    // 2로 나누어 떨어지면 2로 나누기
    // 3으로 나누어 떨어지면 3으로 나누기
    // 1 빼기
// 위의 연산을 통해 1로 만들 때 필요한 최소한의 연산 횟수를 출력하는 프로그램을 작성하세요.

// 입출력 예시
// n: 2
// 출력: 1

// n: 9
// 출력: 2

public class Practice1 {
    public static int solution(int n) {
        // dp 메모리
        int[] dp = new int[n + 1];

        // 각 연산 상황에서의 최소 연산 횟수 업데이트
        for (int i = 2; i <= n; i++) {
            // 빼기 1의 경우
            dp[i] = dp[i - 1] + 1;
            
            // 2로 나누어 떨어지는 경우 비교
            if (i % 2 == 0) {
                dp[i] = Math.min(dp[i], dp[i / 2] + 1);
            }
            
            // 3으로 나누어 떨어지는 경우 비교
            if (i % 3 == 0) {
                dp[i] = Math.min(dp[i], dp[i / 3] + 1);
            }
        }

        return dp[n];
    }

    public static void main(String[] args) {
        // Test code
        System.out.println(solution(2));    // 1
        System.out.println(solution(4));    // 2
        System.out.println(solution(6));    // 2
        System.out.println(solution(9));    // 2
        System.out.println(solution(10));   // 3
    }
}

1
2
2
2
3

// Practice
// 수열 arr 이 주어졌을 때,
// 부분 수열 중 증가하는 부분이 가장 긴 길이를 출력하는 프로그램을 작성하세요.

// 입출력 예시
// arr: {10, 20, 30, 10, 50, 10}
// 출력: 4

public class Practice2 {
    public static int solution(int[] arr) {
        int n = arr.length;
        int[] dp = new int[n + 1];

        int result = 0;
        for (int i = 1; i <= n; i++) {
            // 우선 현재 위치에서의 부분 수열 길이 1로 두고 증가하는 경우 업데이트
            dp[i] = 1;
            for (int j = 1; j < i; j++) {
                // 증가하는 부분 수열 case 에서의 dp 업데이트
                if (arr[j - 1] < arr[i - 1]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            result = Math.max(result, dp[i]);
        }

        return result;
    }

    public static void main(String[] args) {
        // Test code
        int[] arr = new int[]{10, 20, 30, 10, 50, 10};
        System.out.println(solution(arr));
    }
}

4

// Practice
// 배낭에 물품을 담으려고 한다.
// 배낭에는 k 무게 만큼의 물품을 담을 수 있다.
// n 개의 물품이 주어지고 이 물품의 무게와 가치 정보가 items 2차원 배열에 주어졌을 때,
// 최대 가치가 되도록 물품을 담았을 때의 가치를 출력하는 프로그램을 작성하세요.

// 입출력 예시
// items: { {6, 13}, {4, 8}, {3, 6}, {5, 12} }
// n: 4
// k: 7
// 출력: 14


public class Practice3 {

    public static int solution(int[][] items, int n, int k) {
        int[][] dp = new int[n + 1][k + 1];

        // n 개의 물품에 대해 모든 경우의 수 dp 진행
        for (int i = 0; i < n; i++) {
            // 무게 1 ~ k 상황에 대한 계산
            for (int j = 1; j <= k; j++) {
                // 물품을 넣을 수 없을 때는 그 이전의 기록된 가치 가져옴
                if (items[i][0] > j) {
                    dp[i + 1][j] = dp[i][j];
                }
                // 물품을 넣을 수 있는 경우,
                // 이전의 기록된 가치와 현재 담을 수 있는 물품의 가치 비교하여 큰 값으로 업데이트
                else {
                    dp[i + 1][j] = Math.max(dp[i][j], dp[i][j - items[i][0]] + items[i][1]);
                }
            }
        }

        return dp[n][k];
    }

    public static void main(String[] args) {
        // Test code
        int[][] items = { {6, 13}, {4, 8}, {3, 6}, {5, 12} };
        System.out.println(solution(items, 4, 7));  // 14
    }
}

14

출처 : 제로베이스