분할 정복

분할 정복 (Divide and Conquer)

큰 문제를 작은 부분 문제로 나누어 해결하는 방법- 합병 정렬, 퀵 정렬, 이진 검색, … 분할 정복 과정

1. 문제를 하나 이상의 작은 부분들로 분할
2. 부분들을 각각 정복
3. 부분들의 해답을 통합하여 원래 문제의 답을 구함

분할 정복의 장/단점

장점 문제를 나누어 처리하며 어려운 문제 해결 가능 병렬처리에 이점이 있음 단점 메모리를 많이 사용 (재귀 호출 구조)

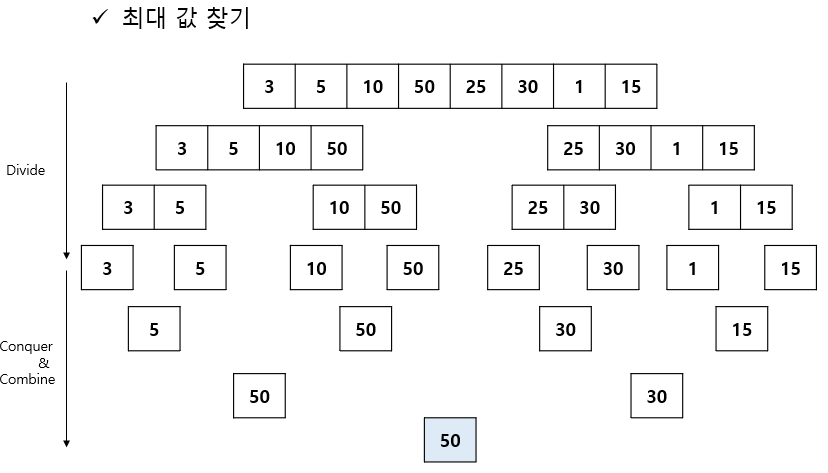
분할 정복 예시 (1)

분할 정복 예시 (2)

public class Main {

    public static int getMax(int[] arr, int left, int right) {
        int m = (left + right) / 2;

        if (left == right) {
            return arr[left];
        }

        left = getMax(arr, left, m);
        right = getMax(arr, m + 1, right);

        return (left > right) ? left : right;
    }


    public static void main(String[] args) {
        int arr[] = {3, 5, 10, 50, 25, 30, 1, 15};
        System.out.println(getMax(arr, 0, arr.length - 1));
    }
}

50

문제풀이

// Practice1
// 정수형 배열 nums 가 주어졌다.
// 연속된 부분 배열의 합 중 가장 큰 값을 출력하세요.

// 입출력 예시
// nums: -5, 0, -3, 4, -1, 3, 1, -5, 8
// 출력: 10

// nums: 5, 4, 0, 7, 8
// 출력: 24

public class Practice1 {

    public static int solution(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }

        return divideSubArray(nums, 0, nums.length - 1);
    }

    public static int divideSubArray(int[] nums, int left, int right) {
        if (left == right) {
            return nums[left];
        }

        // 좌우측 분할
        int mid = left + (right - left) / 2;
        int maxLeft = divideSubArray(nums, left, mid);
        int maxRight = divideSubArray(nums, mid + 1, right);

        // Conquer
        int maxArr = getMaxSubArray(nums, left, mid, right);

        return Math.max(maxLeft, Math.max(maxRight, maxArr));
    }

    public static int getMaxSubArray(int[] nums, int left, int mid, int right) {
        int sumLeft = 0;
        int maxLeft = Integer.MIN_VALUE;

        for (int i = mid; i >= left; i--) {
            sumLeft += nums[i];
            maxLeft = Math.max(maxLeft, sumLeft);
        }

        int sumRight = 0;
        int maxRight = Integer.MIN_VALUE;

        for (int i = mid + 1; i <= right; i++) {
            sumRight += nums[i];
            maxRight = Math.max(maxRight, sumRight);
        }

        return maxLeft + maxRight;
    }

    public static void main(String[] args) {
        // Test code
        int[] nums = {-5, 0, -3, 4, -1, 3, 1, -5, 8};
        System.out.println(solution(nums));

        nums = new int[]{5, 4, 0, 7, 8};
        System.out.println(solution(nums));
    }
}

10
24

// Practice2
// 2차원 정수형 배열 lists 가 주어졌다.
// lists[i] 에는 각 링크드 리스트의 원소 정보가 들어 있고,
// 원소들은 오름차순 정렬된 상태이다.
// 모든 링크드 리스트를 하나의 정렬된 링크드 리스트로 합병하세요.

// 입출력 예시
// lists: { {2, 3, 9}, {1, 5, 7}, {3, 6, 7, 11} }
// 출력: 1 -> 2 -> 3 -> 3 -> 5 -> 6 -> 7 -> 7 -> 9 -> 11


class Node {
    int val;
    Node next;

    Node(int val) {
        this.val = val;
        this.next = null;
    }
}

public class Practice2 {
    public static Node solution(Node[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }

        return divideList(lists, 0, lists.length - 1);
    }

    public static Node divideList(Node[] lists, int left, int right) {
        if (left == right) {
            return lists[left];
        }
        
        // 링크드 리스트 좌우 분할
        int mid = left + (right - left) / 2;
        Node l1 = divideList(lists, left, mid);
        Node l2 = divideList(lists, mid + 1, right);

        return mergeList(l1, l2);
    }

    public static Node mergeList(Node l1, Node l2) {
        if (l1 == null) {
            return l2;
        }

        if (l2 == null) {
            return l1;
        }

        Node merge = new Node(0);
        Node cur = merge;
        while (l1 != null && l2 != null) {
            // l1 쪽이 작으면 해당 값으로 설정 후 l1 은 한 칸 이동
            if (l1.val < l2.val) {
                cur.next = l1;
                l1 = l1.next;
            } else {
                // l2 쪽이 작은 경우
                cur.next = l2;
                l2 = l2.next;
            }
            cur = cur.next;
        }
        
        // 남은 쪽 연결
        if (l1 != null) {
            cur.next = l1;
        }

        if (l2 != null) {
            cur.next = l2;
        }

        return merge.next;
    }

    // 문제에 주어진 2차원 배열을 링크드 리스트로 구성
    public static void setUpLinkedList(Node[] node, int[][] lists) {
        for (int i = 0; i < lists.length; i++) {
            node[i] = new Node(lists[i][0]);
        }

        for (int i = 0; i < lists.length; i++) {
            Node cur = node[i];
            for (int j = 1; j < lists[i].length; j++) {
                cur.next = new Node(lists[i][j]);
                cur = cur.next;
            }
        }
    }

    // 결과 출력 부분
    public static void printList(Node node) {
        Node cur = node;
        while (cur.next != null) {
            System.out.print(cur.val + " -> ");
            cur = cur.next;
        }
        System.out.println(cur.val);
    }

    public static void main(String[] args) {
        // Test code
        int[][] lists = { {2, 3, 9}, {1, 5, 7}, {3, 6, 7, 11} };
        Node[] node = new Node[lists.length];
        setUpLinkedList(node, lists);
        Node combinedNode = solution(node);
        printList(combinedNode);
    }
}

1 -> 2 -> 3 -> 3 -> 5 -> 6 -> 7 -> 7 -> 9 -> 11

출처 : 제로베이스