알고리즘 복잡도

알고리즘 복잡도

복잡도 (Complexity)

알고리즘 성능을 나타내는 척도
시간 복잡도 (Time Complexity)
알고리즘의 필요 연산 횟수
공간 복잡도 (Space Complexity)
알고리즘의 필요 메모리
시간 복잡도와 공간 복잡도는 Trade-off 관계

시간 복잡도 (Time Complexity)

어떤 문제를 해결하기 위한 알고리즘의 필요 연산 횟수
빅오(Big-O) 표기법을 통해 나타냄

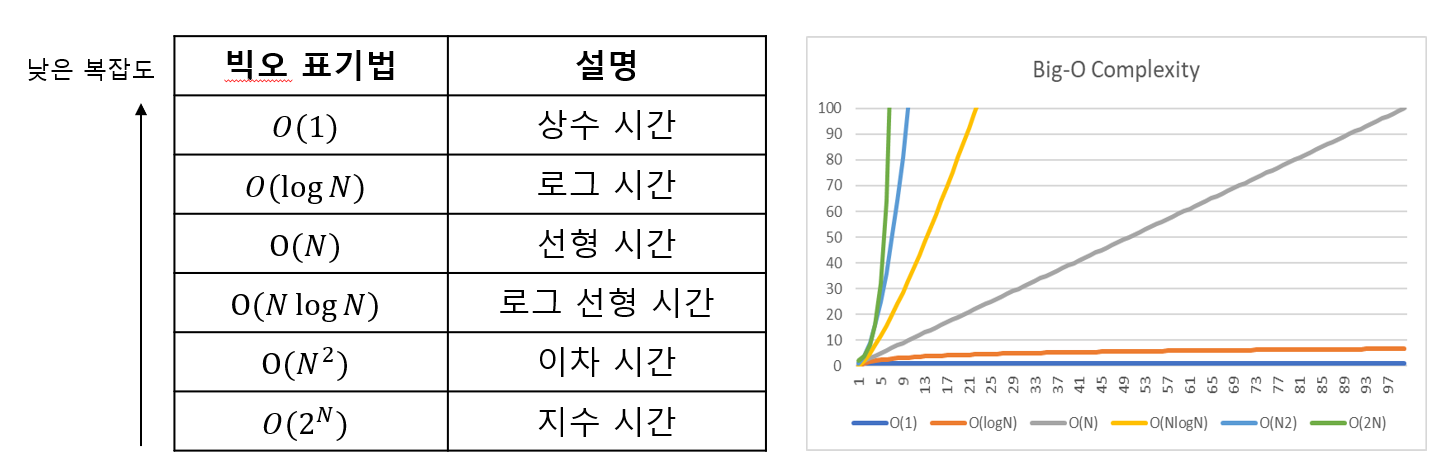
공간 복잡도

어떤 문제를 해결하기 위한 알고리즘의 필요 메모리 사용량
빅오 표기법을 통해 나타냄
일반적으로 메모리 사용량 기준은 MB 단위
int[] a = new int[1000]; // 4KB
int[][] a = new int[1000][1000] // 4MB

public class Practice7 {
    static int fibonacci(int n) {
        if (n < 3) {
            return 1;
        }
        return fibonacci(n - 2) + fibonacci(n - 1);
    }

    static int factorial(int n) {
        if (n < 1) {
            return 1;
        }
        return n * factorial(n - 1);
    }

    public static void main(String[] args) {
        //1. 시간 복잡도
        System.out.println("== 시간 복잡도==");

        //O(1)
        System.out.println("== O(1) ==");
        System.out.println("hello");

        //O(logN)
        System.out.println("== O(logN) ==");
        for (int i = 1; i < 16; i *= 2) {
            System.out.println("hello");
        }

        //O(N)
        System.out.println("== O(N) ==");
        for (int i = 0; i < 2; i++) {
            System.out.println("hello");
        }

        //O(NlogN)
        System.out.println("== O(NlogN) ==");
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                System.out.println("hello ");
            }
            System.out.println();
        }

        //O(2^N)
        System.out.println("== O(2^N) ==");
        //피보나치 재귀
        //1, 1, 2, 3, 5, 8, 13, . . .
        System.out.println(fibonacci(6));

        //2. 공간 복잡도
        System.out.println("== 공간 복잡도 ==");
        //O(N)
        System.out.println("== O(N) ==");
        int n = 3;
        System.out.println(factorial(n));

        //O(1)
        System.out.println("== O(1) ==");
        int result = 1;
        for (int i = 1; i <= n; i++) {
            result *= i;
        }
        System.out.println(result);
    }
}

== 시간 복잡도==
== O(1) ==
hello
== O(logN) ==
hello
hello
hello
hello
== O(N) ==
hello
hello
== O(NlogN) ==
hello 
hello 

hello 
hello 

== O(2^N) ==
8
== 공간 복잡도 ==
== O(N) ==
6
== O(1) ==
6

출처 : 제로베이스