Red-Black 트리
Red-Black 트리
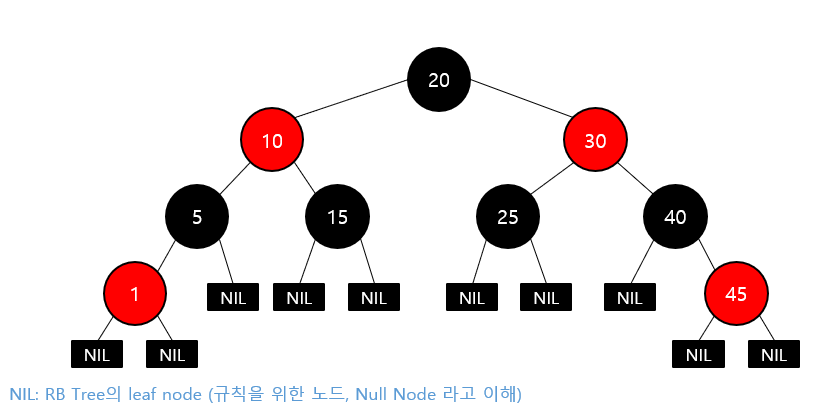
조건
root 노드와 leaf 노드의 색은 black
red 색 노드의 자식은 black (double red 불가)
모든 leaf 노드에서 root 노드까지 가는 경로의 black 노드 수는 같음
조건이 깨지는 상황에서 Rebalancing
Red-Black 트리 – 삽입(1)
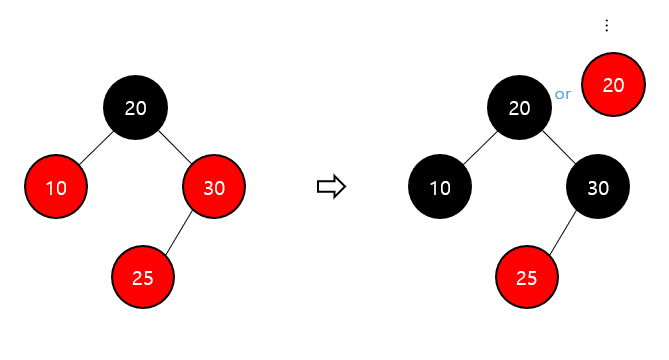
노드 삽입 후 double red 발생 case 1
부모 노드의 형제 노드가 red일 때
Recoloring 진행
삽입한 노드의 부모와 부모의 형제 노드를 black으로 변경
부모의 부모 노드를 red로 변경
부모의 부모 노드가 root인지 double red인지에 따라 조정 진행
Red-Black 트리 – 삽입(2)
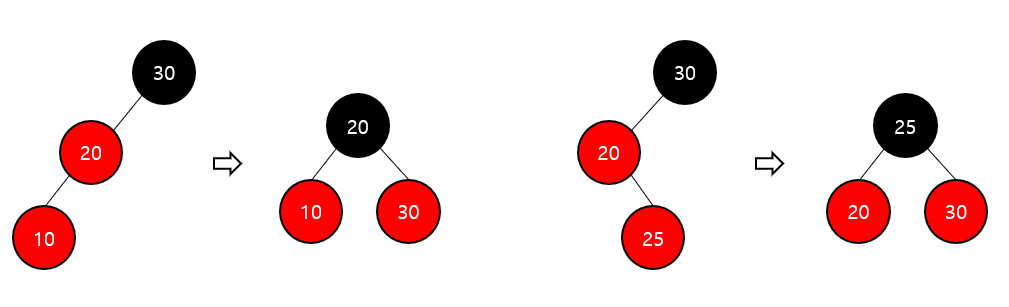
노드 삽입 후 double red 발생 case 2
부모 노드의 형제 노드가 black 이거나 없을 때
Restructuring 진행
조정 대상: 삽입한 노드, 부모 노드, 부모의 부모 노드
조정 대상 노드들을 오름차순 정렬
가운데 노드를 부모 노드로 선정하고 black으로 변경
나머지 두 노드를 자식 노드로 두고 red로 변경
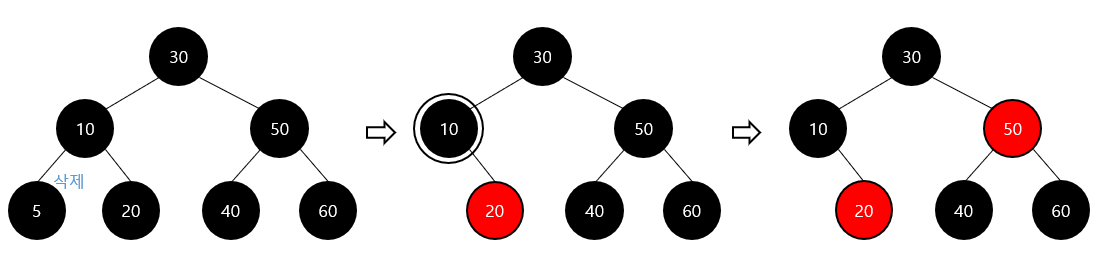
Red-Black 트리 – 삭제 (기본)
삭제 대상 노드가 black 이고 그 자리에 오는 노드가 red인 경우
해당 자리로 오는 red 노드를 black으로 변경
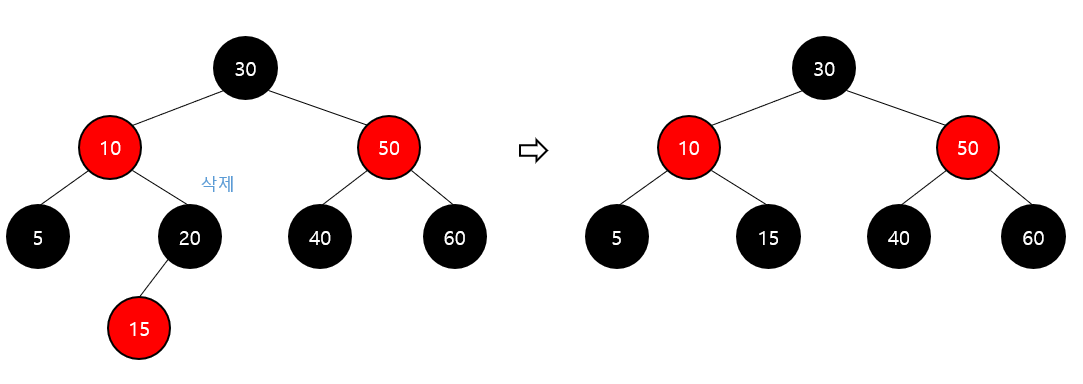
Red-Black 트리 – 삭제 (이중 흑색 1)
삭제 대상 노드가 black, 그 자리에 오는 노드가 black인 경우
이중 흑색 노드의 형제 노드가 black 이고,
형제의 양쪽 자식 모두 black인 경우
형제 노드를 red로 변경
이중 흑색 노드의 검은색 1개를 부모 노드로 전달
부모가 root가 아닌 이중 흑색 노드가 되면 해당 case 반복 진행
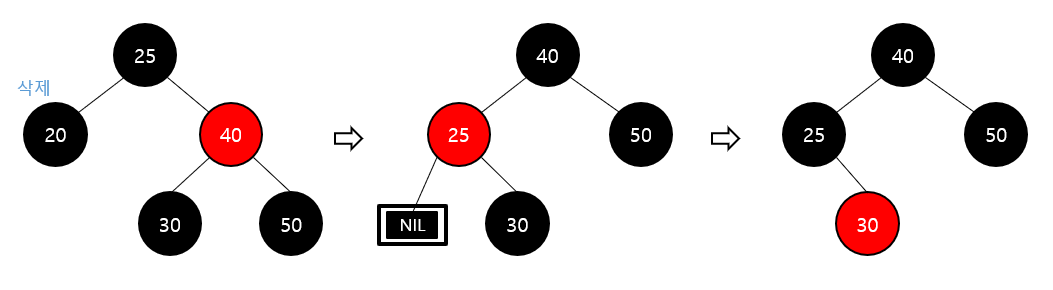
Red-Black 트리 – 삭제 (이중 흑색 2)
Double Black Case 2
이중 흑색 노드의 형제 노드가 red인 경우
형제 노드를 black으로 변경
부모 노드를 red로 변경
부모 노드를 기준으로 왼쪽으로 회전
그 다음 이중 흑색 case 에 따라 반복 진행
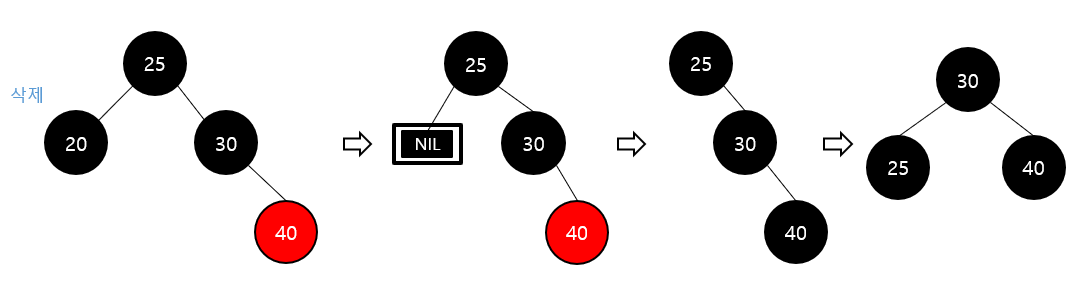
Red-Black 트리 – 삭제 (이중 흑색 3-1)
Double Black Case 3-1
이중 흑색 노드의 형제 노드가 black 이고, 오른쪽 자식이 red인 경우
부모 노드와 형제 노드의 오른쪽 자식 노드를 검은색으로 변경
부모 노드를 기준으로 왼쪽으로 회전
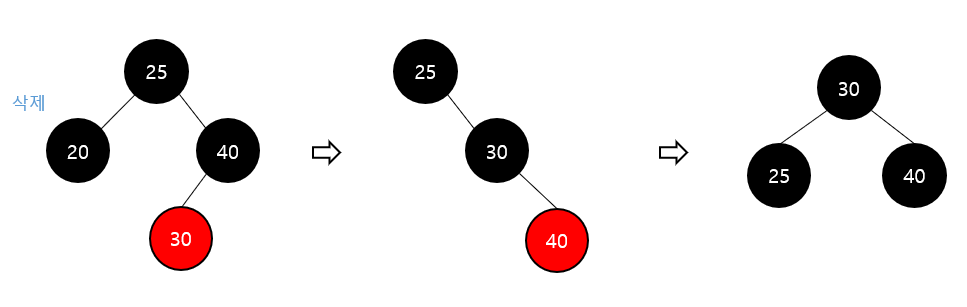
Red-Black 트리 – 삭제 (이중 흑색 3-2)
Double Black Case 3-2
이중 흑색 노드의 형제 노드가 black 이고, 왼쪽 자식이 red인 경우
형제 노드를 red 로 변경
형제 노드의 왼쪽 자식 노드를 black 으로 변경
형제 노드를 기준으로 오른쪽으로 회전
이중 흑색 3-1 case 진행
Red-Black 트리 vs. AVL 트리
알고리즘 시간 복잡도
둘 다 O(logN)
균형 수준
AVL 트리 가 Red-Black 트리 보다 좀 더 엄격하게 균형 잡음
Red-Black 트리는 색으로 구분하는 경우로 인해 회전 수가 감소
실 사용 시,
Tree 체계가 잡힌 후, 탐색이 많은 경우에는 AVL 트리 가 유리
삽입, 삭제가 빈번한 경우에는 Red-Black 트리 가 유리
// 비선형 자료구조 - 이진 탐색 트리_3
// Red-Black 트리 - 삽입
import java.util.LinkedList;
import java.util.Queue;
class Node {
int key;
int color;
Node left;
Node right;
Node parent;
public Node(int key, int color, Node left, Node right, Node parent) {
this.key = key;
this.color = color;
this.left = left;
this.right = right;
this.parent = parent;
}
}
class RedBlackTree {
static final int BLACK = 0;
static final int RED = 1;
Node head;
public void insert(int key) {
Node checkNode = null;
if (this.head == null) {
// 처음 헤드는 Black
this.head = new Node(key, BLACK, null, null, null);
} else {
Node cur = this.head;
// 추가할 위치 찾아 추가하는 부분
while (true) {
Node pre = cur;
if (key < cur.key) {
// 왼쪽 자식 노드 쪽으로 추가
cur = cur.left;
if (cur == null) {
// 추가할 때는 우선 Red
pre.left = new Node(key, RED, null, null, pre);
// 추가한 노드를 re-balancing 대상의 노드로 짚어줌
checkNode = pre.left;
break;
}
} else {
cur = cur.right;
if (cur == null) {
pre.right = new Node(key, RED, null, null, pre);
checkNode = pre.right;
break;
}
}
}
// 추가 후 re-balancing
reBalance(checkNode);
}
}
public void reBalance(Node node) {
// 추가한 노드의 부모가 있고 그 부모가 red 일 때 조정 필요
while (node.parent != null && node.parent.color == RED) {
Node sibling = null;
// 부모 노드의 형제 노드 찾기
if (node.parent == node.parent.parent.left) {
sibling = node.parent.parent.right;
} else {
sibling = node.parent.parent.left;
}
// 부모 노드의 형제 노드가 Red 일 때 re-coloring
if (sibling != null && sibling.color == RED) {
// 부모 노드 black 으로 변경
node.parent.color = BLACK;
// 부모 노드의 형제 노드 black 으로 변경
sibling.color = BLACK;
// 부모의 부모 노드는 red 로 변경
node.parent.parent.color = RED;
// 부모 노드가 root 인 경우는 다시 black 으로 바꾸고 break
if (node.parent.parent == this.head) {
node.parent.parent.color = BLACK;
break;
} else { // 부모 노드가 root 가 아닌 경우는 double red 재발생 할 수 있으므로 반복 검사
node = node.parent.parent;
continue;
}
} else { // 부모 노드의 형제 없거나 black 일 때, re-structuring
if (node.parent == node.parent.parent.left) {
// lr case 인 경우 우선 ll case 가 되도록 회전
if (node == node.parent.right) {
node = node.parent;
leftRotate(node);
}
// 부모 노드는 black 으로 변경
node.parent.color = BLACK;
// 부모의 부모 노드는 red 로 변경
node.parent.parent.color = RED;
rightRotate(node.parent.parent);
} else if (node.parent == node.parent.parent.right) {
// rl case 인 경우 rr case 가 되도록 회전
if (node == node.parent.left) {
node = node.parent;
rightRotate(node);
}
node.parent.color = BLACK;
node.parent.parent.color = RED;
leftRotate(node.parent.parent);
}
break;
}
}
}
public void leftRotate(Node node) {
// node 가 head 인 경우 회전 후 head 교체
if (node.parent == null) {
Node rNode = this.head.right;
this.head.right = rNode.left;
rNode.left.parent = this.head;
this.head.parent = rNode;
rNode.left = this.head;
rNode.parent = null;
this.head = rNode;
} else {
// 회전하기 전 자식 노드있는 경우 이동하는 작업
if (node == node.parent.left) {
node.parent.left = node.right;
} else {
node.parent.right = node.right;
}
node.right.parent = node.parent;
node.parent = node.right;
if (node.right.left != null) {
node.right.left.parent = node;
}
node.right = node.right.left;
node.parent.left = node;
}
}
public void rightRotate(Node node) {
// node 가 head 인 경우 회전 후 head 교체
if (node.parent == null) {
Node lNode = this.head.left;
this.head.left = lNode.right;
lNode.right.parent = this.head;
this.head.parent = lNode;
lNode.right = this.head;
lNode.parent = null;
this.head = lNode;
} else {
if (node == node.parent.left)
node.parent.left = node.left;
else
node.parent.right = node.left;
node.left.parent = node.parent;
node.parent = node.left;
if (node.left.right != null)
node.left.right.parent = node;
node.left = node.left.right;
node.parent.right = node;
}
}
public void levelOrder(Node node) {
char[] color = {'B', 'R'};
Queue<Node> queue = new LinkedList();
queue.add(node);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.print("[" + color[cur.color] + "]" + cur.key + " ");
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
System.out.println();
}
}
public class Practice1 {
public static void main(String[] args) {
// Test code
RedBlackTree rbTree = new RedBlackTree();
rbTree.insert(20);
rbTree.insert(10);
rbTree.insert(30);
rbTree.levelOrder(rbTree.head);
rbTree.insert(25);
rbTree.levelOrder(rbTree.head);
rbTree.insert(5);
rbTree.insert(7);
rbTree.levelOrder(rbTree.head);
rbTree.insert(20);
rbTree.levelOrder(rbTree.head);
}
}
[B]20 [R]10 [R]30
[B]20 [B]10 [B]30 [R]25
[B]20 [B]7 [B]30 [R]5 [R]10 [R]25
[B]20 [B]7 [B]25 [R]5 [R]10 [R]20 [R]30
강사님이 강의에서 코딩테스트에서 레드블랙트리를 구현하라는 문제는 나오지 않을꺼지만 개념지식, 삽입에 대한 코드 작성은 한번 해보면 좋을것 같다해서 따라 작성해보고 스스로 코드 이해작업은 하지 않았음.
출처 : 제로베이스

Leave a comment